MD5算法与实现

背景
MD5全称Message-Digest Algorithm,就是信息摘要算法。是一种被广泛使用的密码散列函数,可以产生出一个128位的散列值,它是由美国密码学家Ron Rivest开发的,于1992年公开。最开始算法是MD,很快出现MD2,不过算法很脆弱,又改为研究MD3,不过最终研发失败。接下来又出现MD4,但仍不理想,最后研发出MD5,成为一个全世界广泛使用的算法。
如今,MD5被证实存在一系列弱点,可以被加以破解,同时也无法防止碰撞,所以已经不适合安全认证。但是,MD5算法因其普遍、稳定、快速的特点,仍广泛应用于普通数据的错误检查领域。
作为一个经典算法,这里就详细梳理一下整个流程。MD5标准文档见这里
详细步骤
填充
第一步是在初始消息中填充信息,使其达到一个要求的长度,即比512位的倍数少64位。如原始消息是1000位,512*3=1536,1536-64=1472,所以要填充472位。填充的内容是1个1和多个0
填充总是要进行的,即使消息长度已经比512的倍数少64位,仍要填充512位
添加长度
计算源消息的长度,表示成64位填充到末尾。如果消息的长度大于2^64,则使用低64位填充,即len mod 2^64
添加完之后,整体长度为512的倍数
分块
将输入以512位一组分块
初始化链接变量
初始化4个32位数字,16进制表示如下
A = 0x67452301
B = 0xEFCDAB89
C = 0x98BADCFE
D = 0x10325476处理块
前面都是初始化操作,这里开始才是算法开始
复制
将4个初始化变量复制到4个变量abcd中,这四个变量组成一个128位寄存器,用于表示中间结果和最终结果
分解
将每块512位分解为16个子块,每个子块32位
轮次迭代
主循环有4轮,每轮有16次操作。每次操作对abcd的其中三个做一次非线性运算P,然后将所得结果加上第四个变量、一个子块和一个常数。再将所得结果向左循环移位,最后加上abcd的其中给一个,最后用该结果取代abcd其中之一。如下图所示
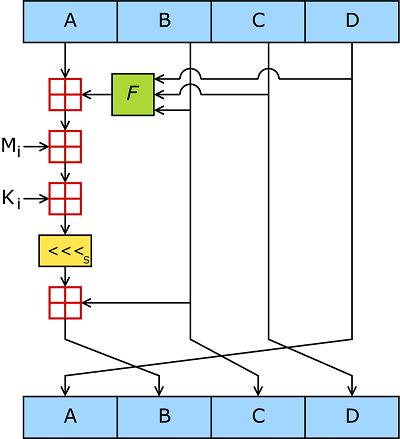
表示成数学表达式如下
a = b + ((a + P(b,c,d) + M[i] + t[k])<<<s)P的每一轮操作如下:
| 轮次 | P |
|---|---|
| 1 | (b AND c) OR ((NOT b) AND b) |
| 2 | (b AND d) OR (c AND (NOT d) |
| 3 | b XOR c XOR d |
| 4 | C XOR (b OR (NOTd) |
轮次操作中常量t[i] = 4294967296*abs(sin(i))的整数部分。下面我们给出每一步详细操作:
首先定义P的4种运算:
F( X ,Y ,Z ) = ( X & Y ) | ( (~X) & Z )
G( X ,Y ,Z ) = ( X & Z ) | ( Y & (~Z) )
H( X ,Y ,Z ) =X ^ Y ^ Z
I( X ,Y ,Z ) =Y ^ ( X | (~Z) )
再定义4个函数:
FF(a ,b ,c ,d ,Mj ,s ,ti ) : a = b + ( (a + F(b,c,d) + Mj + ti) << s)
GG(a ,b ,c ,d ,Mj ,s ,ti ) : a = b + ( (a + G(b,c,d) + Mj + ti) << s)
HH(a ,b ,c ,d ,Mj ,s ,ti ) : a = b + ( (a + H(b,c,d) + Mj + ti) << s)
II(a ,b ,c ,d ,Mj ,s ,ti ) : a = b + ( (a + I(b,c,d) + Mj + ti) << s)
这4轮64步分别如下:
第一轮:
FF(a ,b ,c ,d ,M0 ,7 ,0xd76aa478 )
FF(d ,a ,b ,c ,M1 ,12 ,0xe8c7b756 )
FF(c ,d ,a ,b ,M2 ,17 ,0x242070db )
FF(b ,c ,d ,a ,M3 ,22 ,0xc1bdceee )
FF(a ,b ,c ,d ,M4 ,7 ,0xf57c0faf )
FF(d ,a ,b ,c ,M5 ,12 ,0x4787c62a )
FF(c ,d ,a ,b ,M6 ,17 ,0xa8304613 )
FF(b ,c ,d ,a ,M7 ,22 ,0xfd469501)
FF(a ,b ,c ,d ,M8 ,7 ,0x698098d8 )
FF(d ,a ,b ,c ,M9 ,12 ,0x8b44f7af )
FF(c ,d ,a ,b ,M10 ,17 ,0xffff5bb1 )
FF(b ,c ,d ,a ,M11 ,22 ,0x895cd7be )
FF(a ,b ,c ,d ,M12 ,7 ,0x6b901122 )
FF(d ,a ,b ,c ,M13 ,12 ,0xfd987193 )
FF(c ,d ,a ,b ,M14 ,17 ,0xa679438e )
FF(b ,c ,d ,a ,M15 ,22 ,0x49b40821 )
第二轮
GG(a ,b ,c ,d ,M1 ,5 ,0xf61e2562 )
GG(d ,a ,b ,c ,M6 ,9 ,0xc040b340 )
GG(c ,d ,a ,b ,M11 ,14 ,0x265e5a51 )
GG(b ,c ,d ,a ,M0 ,20 ,0xe9b6c7aa )
GG(a ,b ,c ,d ,M5 ,5 ,0xd62f105d )
GG(d ,a ,b ,c ,M10 ,9 ,0x02441453 )
GG(c ,d ,a ,b ,M15 ,14 ,0xd8a1e681 )
GG(b ,c ,d ,a ,M4 ,20 ,0xe7d3fbc8 )
GG(a ,b ,c ,d ,M9 ,5 ,0x21e1cde6 )
GG(d ,a ,b ,c ,M14 ,9 ,0xc33707d6 )
GG(c ,d ,a ,b ,M3 ,14 ,0xf4d50d87 )
GG(b ,c ,d ,a ,M8 ,20 ,0x455a14ed )
GG(a ,b ,c ,d ,M13 ,5 ,0xa9e3e905 )
GG(d ,a ,b ,c ,M2 ,9 ,0xfcefa3f8 )
GG(c ,d ,a ,b ,M7 ,14 ,0x676f02d9 )
GG(b ,c ,d ,a ,M12 ,20 ,0x8d2a4c8a )
第三轮
HH(a ,b ,c ,d ,M5 ,4 ,0xfffa3942 )
HH(d ,a ,b ,c ,M8 ,11 ,0x8771f681 )
HH(c ,d ,a ,b ,M11 ,16 ,0x6d9d6122 )
HH(b ,c ,d ,a ,M14 ,23 ,0xfde5380c )
HH(a ,b ,c ,d ,M1 ,4 ,0xa4beea44 )
HH(d ,a ,b ,c ,M4 ,11 ,0x4bdecfa9 )
HH(c ,d ,a ,b ,M7 ,16 ,0xf6bb4b60 )
HH(b ,c ,d ,a ,M10 ,23 ,0xbebfbc70 )
HH(a ,b ,c ,d ,M13 ,4 ,0x289b7ec6 )
HH(d ,a ,b ,c ,M0 ,11 ,0xeaa127fa )
HH(c ,d ,a ,b ,M3 ,16 ,0xd4ef3085 )
HH(b ,c ,d ,a ,M6 ,23 ,0x04881d05 )
HH(a ,b ,c ,d ,M9 ,4 ,0xd9d4d039 )
HH(d ,a ,b ,c ,M12 ,11 ,0xe6db99e5 )
HH(c ,d ,a ,b ,M15 ,16 ,0x1fa27cf8 )
HH(b ,c ,d ,a ,M2 ,23 ,0xc4ac5665 )
第四轮
II(a ,b ,c ,d ,M0 ,6 ,0xf4292244 )
II(d ,a ,b ,c ,M7 ,10 ,0x432aff97 )
II(c ,d ,a ,b ,M14 ,15 ,0xab9423a7 )
II(b ,c ,d ,a ,M5 ,21 ,0xfc93a039 )
II(a ,b ,c ,d ,M12 ,6 ,0x655b59c3 )
II(d ,a ,b ,c ,M3 ,10 ,0x8f0ccc92 )
II(c ,d ,a ,b ,M10 ,15 ,0xffeff47d )
II(b ,c ,d ,a ,M1 ,21 ,0x85845dd1 )
II(a ,b ,c ,d ,M8 ,6 ,0x6fa87e4f )
II(d ,a ,b ,c ,M15 ,10 ,0xfe2ce6e0 )
II(c ,d ,a ,b ,M6 ,15 ,0xa3014314 )
II(b ,c ,d ,a ,M13 ,21 ,0x4e0811a1 )
II(a ,b ,c ,d ,M4 ,6 ,0xf7537e82 )
II(d ,a ,b ,c ,M11 ,10 ,0xbd3af235 )
II(c ,d ,a ,b ,M2 ,15 ,0x2ad7d2bb )
II(b ,c ,d ,a ,M9 ,21 ,0xeb86d391 )上面是网上大多是文章给出的方法,就是生硬的给出64轮具体操作,但其实每一步都是可以推算的,下面来说一下简单的方法:
首先对于常数,可以通过公式计算,t[i] = 4294967296*abs(sin(i))的整数部分,其中4294967296就是1<<32,即2^32
对于这个长度建议是直接写成常量,不然每次都计算也比较耗时:
private static final int T[] = {
0xd76aa478, 0xe8c7b756, 0x242070db, 0xc1bdceee,
0xf57c0faf, 0x4787c62a, 0xa8304613, 0xfd469501, 0x698098d8,
0x8b44f7af, 0xffff5bb1, 0x895cd7be, 0x6b901122, 0xfd987193,
0xa679438e, 0x49b40821, 0xf61e2562, 0xc040b340, 0x265e5a51,
0xe9b6c7aa, 0xd62f105d, 0x02441453, 0xd8a1e681, 0xe7d3fbc8,
0x21e1cde6, 0xc33707d6, 0xf4d50d87, 0x455a14ed, 0xa9e3e905,
0xfcefa3f8, 0x676f02d9, 0x8d2a4c8a, 0xfffa3942, 0x8771f681,
0x6d9d6122, 0xfde5380c, 0xa4beea44, 0x4bdecfa9, 0xf6bb4b60,
0xbebfbc70, 0x289b7ec6, 0xeaa127fa, 0xd4ef3085, 0x04881d05,
0xd9d4d039, 0xe6db99e5, 0x1fa27cf8, 0xc4ac5665, 0xf4292244,
0x432aff97, 0xab9423a7, 0xfc93a039, 0x655b59c3, 0x8f0ccc92,
0xffeff47d, 0x85845dd1, 0x6fa87e4f, 0xfe2ce6e0, 0xa3014314,
0x4e0811a1, 0xf7537e82, 0xbd3af235, 0x2ad7d2bb, 0xeb86d391
};
对于每次取哪一小组明文,是根据轮次定的,定义j是小轮次,0 <= j < 64:
第一大轮就是按顺序取1~16小组 i = j
第二大轮的计算规则为 i = (1+5*j)%16 即 (j*5+1)&0x0f
第三大轮的计算规则为 i = (5+3*j)%16 即 (j*3+5)&0x0F
第四大轮的计算规则为 i = (7*j)%16 即 (j*7)&0x0F
对于移位,也是根据轮次定的,定义j是小轮次,0 <= j < 64:
第一大轮 从[7, 12, 17, 22]取,j%4
第一大轮 从[5, 9, 14, 20]取,j%4
第一大轮 从[4, 11, 16, 23]取,j%4
第一大轮 从[6, 10, 15, 21]取,j%4
若写到一个数组中:
public static final int S[] = new int[]{
7, 12, 17, 22, 5, 9, 14, 20, 4,
11, 16, 23, 6, 10, 15, 21
};
可以通过如下公式取值:S[(pType << 2) | (j & 3)]) //pType指第几大轮,j指第几小轮
对于每次运算abcd数输入顺序:
可以明显观察到,每一小轮之后,下一轮的输入相当于把abcd做循环右移一位,而P运算的输入固定位bcd,所以做如下交换
a = d;
d = c;
c = b;
b = temp;经过这64步之后,A=a,B=b,C=c,D=d,然后将ABCD作为处理下一明文块的输入
应用
MD5已经广泛使用在为文件传输提供一定的可靠性方面。例如,服务器预先提供一个MD5校验和,用户下载完文件以后,用MD5算法计算下载文件的MD5校验和,然后通过检查这两个校验和是否一致,就能判断下载的文件是否出错。
实现
下面来给出java版本的具体实现,关键步骤有注释,详细代码见这里
public String md5(String msg){
byte[] msgBytes = msg.getBytes();
int msgBytesLen = msgBytes.length;//原始信息长度,单位bit
int numBlock = ((msgBytesLen + 8)>>>6) + 1; //总块数=(原始长度+8bit)/64bit + 1
int totalLen = numBlock << 6; //补全后的长度 = 块数 * 64bit
byte[] padBytes = new byte[totalLen - msgBytesLen]; //需要补的bit数
padBytes[0] = (byte) 0x80; //补一个1和若干个0
long msgLen = (long)msgBytesLen << 3; //计算出多少bit,长度*8
for(int i = 0;i<8;i++){
padBytes[padBytes.length - 8 + i] = (byte) msgLen;//从低位开始写入长度
msgLen >>>= 8;
}
int a = A,b =B,c = C,d = D; //赋值常量
int[] buffer = new int[16]; //每块512位,16个int类型
for (int i = 0;i<numBlock;i++){
int index = i << 6;
for (int j = 0;j<64;j++,index++)
//index是msg的游标,j是buffer的游标,一个int类型存4个byte类型
//从低位开始存
buffer[j >>> 2] = ((int) ((index < msgBytesLen) ? msgBytes[index]
: padBytes[index - msgBytesLen]) << 24)
| (buffer[j >>> 2] >>> 8);
int tempa = a; //记录abcd的临时变量
int tempb = b;
int tempc = c;
int tempd = d;
for (int j = 0;j<64;j++) { //64小轮
int pType = j >>> 4; //判断是第几大轮
int f = 0; //P运算的值
int bufferIndex = j; //buffer的游标
switch (pType){ //定义不同大轮的具体P运算
case 0:
f = (b &c) | (~b & d);
break;
case 1:
f = (b & d) | (c & ~d);
bufferIndex = (bufferIndex*5+1)&0x0f; //明文子组和轮数的关系
break;
case 2:
f = b ^ c ^ d;
bufferIndex = (bufferIndex * 3 + 5) & 0x0F;
break;
case 3:
f = c ^ (b | ~d);
bufferIndex = (bufferIndex * 7) & 0x0F;
break;
}
//运算
int temp = b + Integer.rotateLeft(a + f + buffer[bufferIndex] + T[j], S[(pType << 2) | (j & 3)]);
//交换abcd
a = d;
d = c;
c = b;
b = temp;
}
//分组处理完之后abcd各自累加
a += tempa;
b += tempb;
c += tempc;
d += tempd;
}
//abcd写到16个byte中
byte[] out = new byte[16];
int count = 0;
for (int i = 0;i<4;i++){
int n = (i == 0) ? a : ((i == 1) ? b : ((i == 2) ? c : d));
for (int j = 0;j<4;j++){
out[count++] = (byte)n;
n>>>=8;
}
}
//转为十六进制表示
StringBuffer sb = new StringBuffer();
for (byte bout : out){
sb.append(HEX[(bout>>>4)&0xf]);
sb.append(HEX[bout&0xf]);
}
return sb.toString();
}简单测试后结果正确无误
题图来自unsplash:https://unsplash.com/photos/HsEz1XZ1TO8