分组密码中的算法模式

发表于 更新于 分类于 本文字数： 1.7k 阅读时长 ≈ 2 分钟

算法模式是块加密中一系列步骤中基本，同一种加密方法采用不同的模式会产生不同的密文，安全性也不尽相同

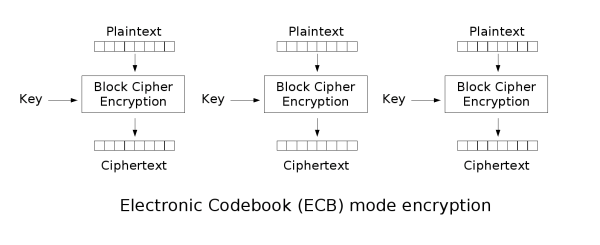
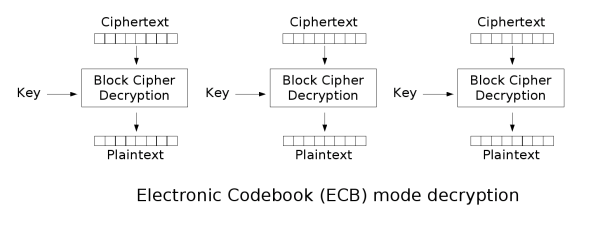
电子密码薄（ECB）模式

这是块加密中最简单的模式，如定义每块为64位，则将明文每64位分一组，之后对每组使用相同的秘钥和加密算法进行单独加密。解密时也是按64位分组，用同样的秘钥和加密方法进行解密即可。这种方法只适合于短消息，因为如果有重复信息，密文也会产生重复，易被攻击。加解密示意图如下：

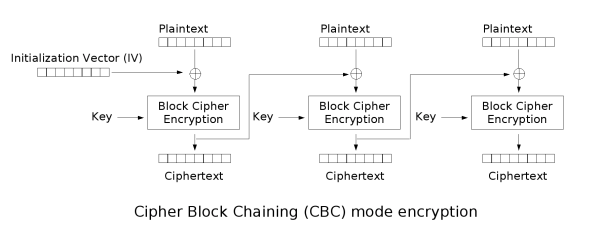
加密块链接（CBC）模式

这种模式的特点是对前一个块加密的结果会影响当前块的加密，确保了每条消息的唯一性。基本过程如下：

  1. 首先随机出一个与分组等长的初始文本块，然后用该文本块和第一个要加密的块做异或运算，并对运算结果进行加密
  2. 加密第二个块时，用第一个块加密之后的密文与第二个块进行异或运算，并对运算结果使用和第一块相同的算法和秘钥进行加密
  3. 依次类推，关键点是，在加密前使用上一块的密文与当前块做异或运算，之后再加密

可以抽象为下面数学表达(Ek表示加密函数，Ci表示明文的第几块)：

示意图如下：

对于解密，首先要了解一下异或运算的一个重要性质，就是连用两次异或后能恢复原值，即 A = A XOR B XOR B。由于这个性质异或就天然的有隐藏和还原信息的功能，所以解密算法如下

  1. 首先对密文块1进行解密，解密后再和加密时使用的初始文本块做异或运算就得到了原文.
  2. 对其他密文块也是一样，先解密，再与前一个密文块做异或，就得到原文

可以抽象为下面数学表达(Dk表示解密函数，Ci表示明文的第几块)：

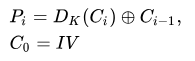
示意图如下：

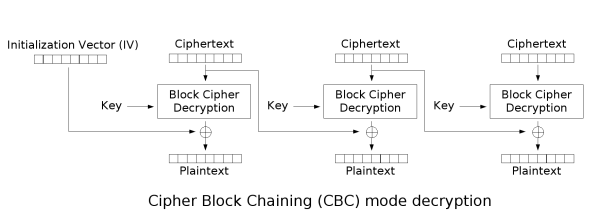
这种模式虽然很好的隐藏了信息，但是由于加密时都要依赖前面的信息，所以只能串行加密。不能并行运算。但是解密时可以并行运算

加密反馈（CFB）模式

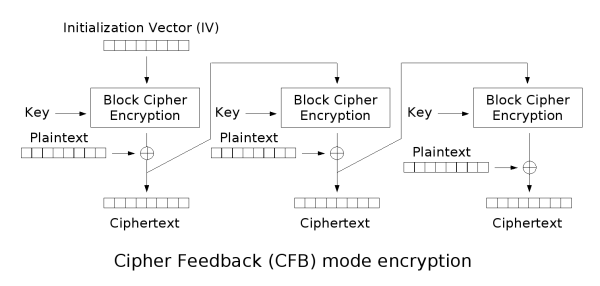
首先并不是所有程序都能处理数据库，如一个输入系统，需要以安全方式在信道中立即传输信息，这就要求数据用更小的单元进行加密（如8位，以byte长度）。所以出现了CFB模式。基本流程如下：

  1. 首先也需要一个64位的初始化向量，并将其放在移位寄存器中，并对该初始化向量进行加密，得到64位的初始密文
  2. 将加密过的初始化向量前j位和明文前j为进行异或，作为密文输出
  3. 将寄存器中的初始化向量左移j位，并将刚才加密的j位拼接到初始化向量尾部
  4. 然后重复上面步骤，即再对寄存器中的新初始化向量加密，随后再加密明文前j位，再进行左移个补充操作，最后再循环

示意图如下：

解密也很简单，由于明文是和移位寄存器中加密过的内容做异或后得到的密文，所以根据异或的性质，只需把密文和移位寄存器（初始内容还是加密时选定初始内容）中加密过的内容再做一次异或就得到明文（注意解密之后，寄存器中内容也要同步移位）示意图如下：

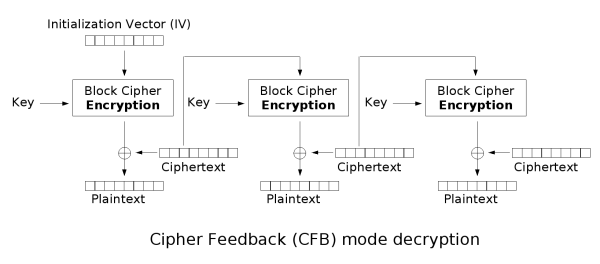
这种模式虽然和CBC很像，但是有一个优点，就是明文是不需要填充为分组的整数倍数长度的，明文和密文有相等长度，且较为灵活。

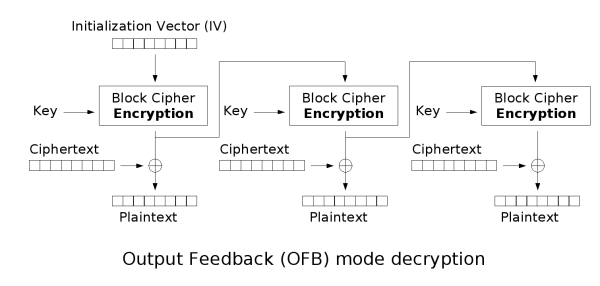
输出反馈（OFB）模式

这种模式和CFB模型类似，但是没有CFB那么复杂，直接看一下示意图比较清晰：

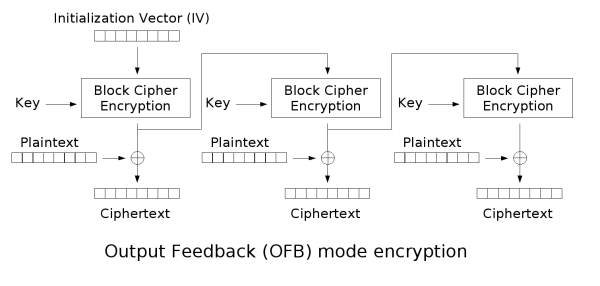
可见主要区别是移位寄存器中的内容不再受密文的影响，而是每次独立进行加密。这样做的一大好处是某一位出错后，仅影响该位的密文，而和后面无关，前面CBC和CFB每次加密都会用到前面的信息，某一位出错将会影响后面所有输出。

解密过程也就相对较简单，将密文和初始向量加密后的信息做异或处理即可，随后也同步更新移位寄存器中内容。示意图如下

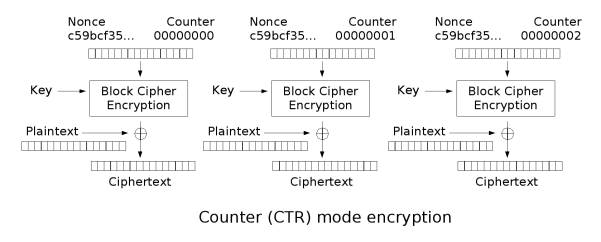
计数器(CTR)模式

这种模式也被成为ICM(Integer Counter Mode)或SIC模式(Segmented Integer Counter)

这种模式类似于OFB模式，只不过将寄存器中的值换做一个计数器，计数器在任意时间产生不同的输出，之后对该输出进行加密，并用加密过的结果和明文异或，得到的结果作为密文。示意图（注意图中计数器的输出采用的是一个初始化向量和整数拼接的方式）如下：

解密方法和OFB类似，不在赘述，直接看示意图

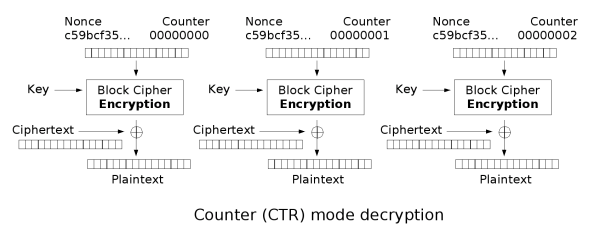
这种方式的一大特点是可以并行加密，由于不同块的计数器输出是可以事先预测的，所以可以实现并行加密。

题图来自unsplash: https://unsplash.com/photos/pdRsf77OBoo